Spherical Trigonometry

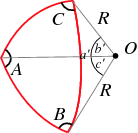
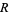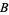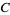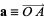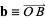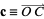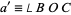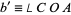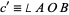Let a spherical triangle be drawn on the surface of a sphere of radius , centered at a point , with vertices , , and . The vectors from the center of the sphere to the vertices are therefore given by , , and . Now, the angular lengths of the sides of the triangle (in radians) are then , , and , and the actual arc lengths of the side are 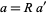, , 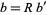and 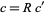. Explicitly,

			(1)
			(2)
			(3)

Now make use of 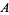, , 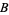and 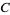 to denote both the vertices themselves and the angles of the spherical triangle at these vertices, so that the dihedral angle between planes  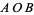and 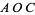 is written 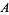, the dihedral angle between planes  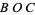and 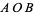 is written 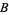, and the dihedral angle between planes  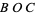and 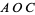 is written 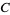. (These angles are sometimes instead denoted 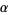, , 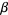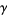; e.g., Gellert et al. 1989)

Consider the dihedral angle 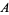 between planes  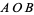and 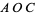, which can be calculated using the dot product of the normals to the planes. Assuming 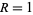, the normals are given by cross products of the vectors to the vertices, so

			(4)
			(5)

However, using a well-known vector identity gives

			(6)
			(7)
			(8)
			(9)

Since these two expressions must be equal, we obtain the identity (and its two analogous formulas)

			(10)
			(11)
			(12)

known as the cosine rules for sides (Smart 1960, pp. 7-8; Gellert et al. 1989, p. 264; Zwillinger 1995, p. 469).

The identity

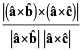			(13)
			(14)
			(15)

where  is the scalar triple product, gives

(16)

so the spherical analog of the law of sines can be written

(17)

(Smart 1960, pp. 9-10; Gellert et al. 1989, p. 265; Zwillinger 1995, p. 469), where 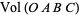 is the volume of thetetrahedron.

The analogs of the law of cosines for the angles of a spherical triangle are given by

			(18)
			(19)
			(20)

(Gellert et al. 1989, p. 265; Zwillinger 1995, p. 470).

Finally, there are spherical analogs of the law of tangents,

			(21)
			(22)
			(23)

(Beyer 1987; Gellert et al. 1989; Zwillinger 1995, p. 470).

Additional important identities are given by

(24)

(Smart 1960, p. 8),

(25)

(Smart 1960, p. 10), and

(26)

(Smart 1960, p. 12).

Let

(27)

be the semiperimeter, then half-angle formulas for sines can be written as

			(28)
			(29)
			(30)