
The surface of revolution of the parabola which is the shape used in the reflectors of automobile headlights (Steinhaus 1999, p. 242; Hilbert and Cohn-Vossen 1999). It is a quadratic surface which can be specified by the Cartesian equation
(1)
|
(2)
| |||
(3)
| |||
(4)
|
The coefficients of the first fundamental form are given by
(5)
| |||
(6)
| |||
(7)
|
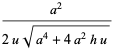 |
(8)
| ||
(9)
| |||
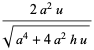 |
(10)
|
(11)
|
(12)
| |||
(13)
|
(14)
|
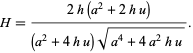 |
(15)
|
(16)
| |||
(17)
|
(18)
| |||
(19)
|