The Euler formula, sometimes also called the Euler identity (e.g., Trott 2004, p. 174), states
 |
(1)
|
where i is the imaginary unit. Note that Euler's polyhedral formula is sometimes also called the Euler formula, as is theEuler curvature formula. The equivalent expression
 |
(2)
|
had previously been published by Cotes (1714).
The special case of the formula with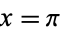 
gives the beautiful identity
gives the beautiful identity |
(3)
|
an equation connecting the fundamental numbers i, pi, e, 1, and 0 (zero), the fundamental operations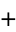 
, 
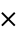, and exponentiation, the most important relation 
, and nothing else. Gauss is reported to have commented that if this formula was not immediately obvious, the reader would never be a first-class mathematician (Derbyshire 2004, p. 202).
, , and exponentiation, the most important relation 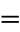, and nothing else. Gauss is reported to have commented that if this formula was not immediately obvious, the reader would never be a first-class mathematician (Derbyshire 2004, p. 202).
The Euler formula can be demonstrated using a series expansion
 |  |  |
(4)
|
 |  |  |
(5)
|
 |  |  |
(6)
|
It can also be demonstrated using a complex integral. Let
 |  |  |
(7)
|
 |  |  |
(8)
|
 |  |  |
(9)
|
 |  |  |
(10)
|
 |  |  |
(11)
|
 |  |  |
(12)
|
so
 |  |  |
(13)
|
 |  |  |
(14)
|
A mathematical joke asks, "How many mathematicians does it take to change a light bulb?" and answers "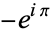
" (which, of course, equals 1).
" (which, of course, equals 1).