We see the columns everywhere around us because they are very important component of structures. Column is the vertical member of a structure which generally takes the compression from the other components mainly, slabs. So the main function is to transfer the vertical load to the lower foundations of the structure. There is other component which is known as the strut, it is again a compression member which takes up the compression or also they may be designed to take up the tension, such members are used in the roof trusses.
The major structural difference: Columns have higher slenderness ratio so, due to more slenderness the columns fail due to buckling in general and the struts fail due to crushing under the action of the compression.
You have to understand the concept of effective length, least radius of gyration and slenderness ratio first to calculate the Euler's buckling load.
Slenderness ratio:
Generally denoted by "r", the slenderness ratio is the ratio of the effective length of the component to the least radius of gyration.
r = L/k
Where L= effective length of a column;( Effective length is the length which participate in the buckling(which actually buckles)
k = Least radius of gyration, which can be computed by the formula given as,
k= (Imin/A)^(1/2) , Where A is the Area of cross section of the column
k= (Imin/A)^(1/2) , Where A is the Area of cross section of the column
and, I = Least moment of inertia
(Note: Least moment of inertia can be taken as the least of the moment of inertia of the cross section about both the axis)
Euler's Formula:
In 1757, mathematician Leonhard Euler created a formula for the buckling load for a column without considering the lateral loads.
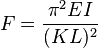
Here F is the load under which a column will just start to buckle.
I is the least moment of Inertia.
K is the effective length factor.
L is the total length of the column
Effective length of a column depends upon the end support conditions of the columns:
a) For both ends pinned effective length is "L". So K = 1
b) For both ends fixed, this is "L/2", so K= 1/2
c) For one end Fixed and other free, this is 2L so, K = 2
d) For one end fixed and other hinge, this is L/1.414 so, K =1/1.414
Effective length of a column depends upon the end support conditions of the columns:
a) For both ends pinned effective length is "L". So K = 1
b) For both ends fixed, this is "L/2", so K= 1/2
c) For one end Fixed and other free, this is 2L so, K = 2
d) For one end fixed and other hinge, this is L/1.414 so, K =1/1.414
If you understand the Euler's formula which is applicable to the columns which fail under buckling, then you can easily understand that this formula is not of much use to the struts which are likely to get failed due to crushing.
In some columns you might have to consider both the factors. Considering the limitation of the Euler's Formula, Rankine gave a formula, known as the
Rankine Gordon-Formula,
1/(critical load) = 1/(crushing load) + 1/(buckling load)
= 1/Pc + 1/Pe (Pe = Euler's Load =F ; Pc = Crushing strength of the material of column)
Or,
Pcr= Pc/[1+ a.(Le/k)^2]
Crushing load can be found by multiplying the crushing strength with the cross section area of the column. Buckling load can be found in the usual manner by Euler formula. Rankine formula is applicable to all types of columns, short as well as long columns.
In some columns you might have to consider both the factors. Considering the limitation of the Euler's Formula, Rankine gave a formula, known as the
Rankine Gordon-Formula,
1/(critical load) = 1/(crushing load) + 1/(buckling load)
= 1/Pc + 1/Pe (Pe = Euler's Load =F ; Pc = Crushing strength of the material of column)
Or,
Pcr= Pc/[1+ a.(Le/k)^2]
Crushing load can be found by multiplying the crushing strength with the cross section area of the column. Buckling load can be found in the usual manner by Euler formula. Rankine formula is applicable to all types of columns, short as well as long columns.
