A second-order algebraic surface given by the general equation
(1)
|
Quadratic surfaces are also called quadrics, and there are 17 standard-form types. A quadratic surface intersectsevery plane in a (proper or degenerate) conic section. In addition, the cone consisting of all tangents from a fixed point to a quadratic surface cuts every plane in a conic section, and the points of contact of this cone with the surface form aconic section (Hilbert and Cohn-Vossen 1999, p. 12).
Examples of quadratic surfaces include the cone, cylinder, ellipsoid, elliptic cone, elliptic cylinder, elliptic hyperboloid,elliptic paraboloid, hyperbolic cylinder, hyperbolic paraboloid, paraboloid, sphere, and spheroid.
Define
![[a h g; h b f; g f c]](http://mathworld.wolfram.com/images/equations/QuadraticSurface/Inline3.gif) |
(2)
| ||
![[a h g p; h b f q; g f c r; p q r d]](http://mathworld.wolfram.com/images/equations/QuadraticSurface/Inline6.gif) |
(3)
| ||
(4)
| |||
(5)
| |||
(6)
|
and 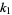 ,
, 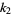 , as
, as 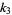 are the roots of
are the roots of
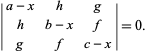 |
(7)
|
Also define
(8)
|
Then the following table enumerates the 17 quadrics and their properties (Beyer 1987).
| surface | equation | ||||
| coincident planes | 1 | 1 | |||
| ellipsoid (imaginary) | 3 | 4 | 1 | ||
| ellipsoid (real) | 3 | 4 | 1 | ||
| elliptic cone (imaginary) | 3 | 3 | 1 | ||
| elliptic cone (real) | 3 | 3 | 0 | ||
| elliptic cylinder (imaginary) | 2 | 3 | 1 | ||
| elliptic cylinder (real) | 2 | 3 | 1 | ||
| elliptic paraboloid | 2 | 4 | 1 | ||
| hyperbolic cylinder | 2 | 3 | 0 | ||
| hyperbolic paraboloid | 2 | 4 | 0 | ||
| hyperboloid of one sheet | 3 | 4 | 0 | ||
| hyperboloid of two sheets | 3 | 4 | 0 | ||
| intersecting planes (imaginary) | 2 | 2 | 1 | ||
| intersecting planes (real) | 2 | 2 | 0 | ||
| parabolic cylinder | 1 | 3 | |||
| parallel planes (imaginary) | 1 | 2 | |||
| parallel planes (real) | 1 | 2 |
Of the non-degenerate quadratic surfaces, the elliptic (and usual) cylinder, hyperbolic cylinder, elliptic (and usual) coneare ruled surfaces, while the one-sheeted hyperboloid and hyperbolic paraboloid are doubly ruled surfaces.