Balance of payments equilibrium occurs when induced balance of payments transactions---those engineered by the government to influence the nominal exchange rate---are zero. This implies that autonomous receipts from exports and the sale of securities abroad equal autonomous payments for imports and the purchase of securities from foreign residents. Since changes in the stock of official reserves of foreign exchange are the method used by the authorities to fix or otherwise manipulate the exchange rate, balance of payments equilibrium requires that the stock of foreign exchange reserves be constant.
Induced transactions are frequent when the exchange rate is fixed---only by chance will autonomous receipts and payments balance. They can also occur when the exchange rate is flexible and the authorities want to influence its movement. But we will concentrate primarily on the fixed exchange rate case here.
The condition of asset equilibrium---the LM equation---can be presented as the equality of the demand and supply of nominal money balances as follows:
1. M = mm H = mm (R + Dsc) = P [ γ − θ ( r* + τ) + ε Y ]
where Y is real income, P is the price level, r* is the real interest rate determined by conditions in the rest of the world, τ is the expected rate of inflation, mm is the money multiplier, R is the stock of official foreign exchange reserves, which can be thought of as the foreign source component of the stock of base money and Dsc is the domestic source component of the stock of base money H. The above equation can be manipulated to present the equilibrium stock of high powered or base money as
2. H = R + Dsc = (P / mm) [ γ − θ ( r* + τ) + ε Y ]
which can be further rearranged to move the stock of foreign exchange reserves R to the left side.
3. R = (1 / mm) P [ γ − θ ( r* + τ) + ε Y ] − Dsc
An increase in the demand for money, given by the P times the expression in the square brackets [..], leads to an increase in the stock of official foreign exchange reserves as the authorities act to maintain the fixed exchange rate. A reduction in the money multiplier increases the stock of base money required to support the existing quantity of money, requiring in an increase in the stock of reserves to provide the additional base money demanded. An increase in Dsc leads to an equal decline in the stock of foreign exchange reserves as the authorities are forced to keep the stock of money unchanged at its desired level to maintain the exchange rate parity.
The authorities are forced to maintain a stock of reserves that will provide domestic residents with their desired money holdings, given the domestic source component. This implies that the commercial banks and the public will have their desired stock of base money. It also means that the authorities can effectively control the stock of official foreign exchange reserves by manipulating the domestic source component---such changes in the stock of reserves can be brought about at no cost in terms of price level changes, or output and employment changes when the price level is fixed. As you should have learned in the previous two lessons, output, income and prices are determined by the conditions of flow equilibrium.
It is evident from Equation 3 above that we must distinguish between two types of balance of payments disequilibria---stock and flow. A one-shot adjustment of the domestic source component or shift in the demand for base money holdings at a moment in time will lead to a shift in the stock of official reserves at that moment in time. The stock of official reserves will typically also be growing or declining at some rate through time---it is this flow of increases or decreases in the stock of reserves that is commonly referred to as the balance of payments surplus or deficit, which can be expressed as
4. ΔR = Δ[(1 / mm) P [ γ − θ ( r* + τ) + ε Y ]] − ΔDsc
where Δ is the change per unit time. Official reserve holdings change through time because the levels of income, prices, and the real interest rate and the money multiplier change through time---the effects of these changes are captured by the major collection of terms in the square brackets to the right of the equal sign. They also change as a result of a change in the domestic source component ΔDsc through time.
Notice that the presence of balance of payments equilibrium is completely independent of the condition of flow equilibrium---indeed, we did not have to include the IS equation in the above discussion. This is the case as long as people are free to buy and sell assets in the international market. There is no relationship of balance of payments equilibrium to equilibrium in the balance of trade---balance of payments equilibrium is entirely a monetary phenomenon. All this changes when we assume that there is zero private international mobility---that private residents are prohibited from purchasing assets from or selling them to foreign residents. In this case, the only domestically held foreign assets are official foreign exchange reserves and the condition of balance of payments equilibrium becomes
ΔR = BT
where BT is the balance of trade---the balance of payments surplus or deficit becomes equal to the balance of trade surplus or deficit. To maintain balance of payments equiibrium the government has to bring about changes in the balance of trade by bringing about changes in the price level or income and employment or allowing the nominal exchange rate to change.The Canadian period of fixed exchange rates between late-1962 and mid-1970 provides an interesting example of the growth of official reserves in relation to base money. Figure 1 presents the two series expressed in millions of Canadian dollars.
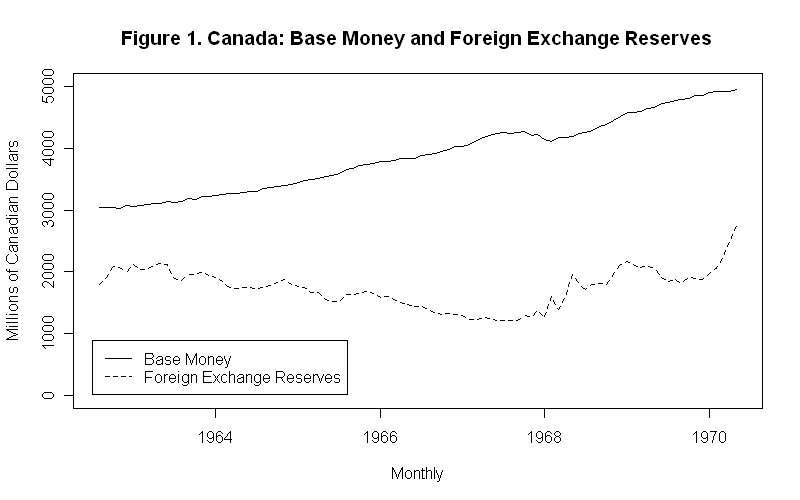
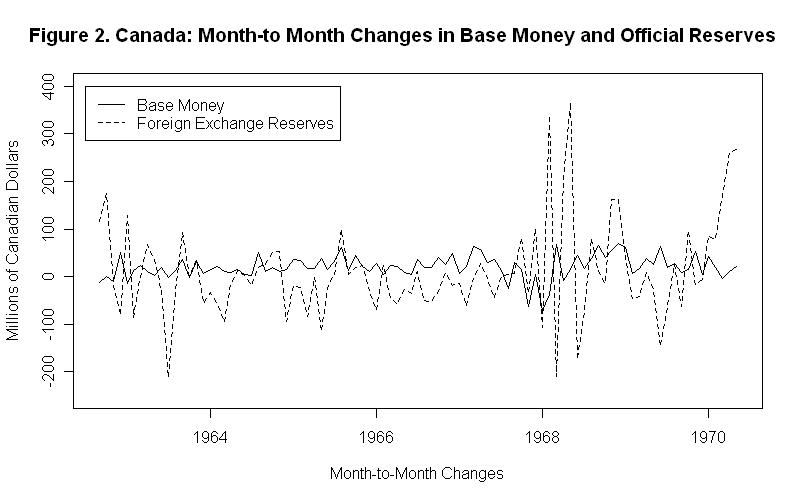
The fact that reserves were more variable than base money suggests that these changes in official reserves were driven in considerable part by changes in the opposite direction in the domestic source component. Since H equals R plus Dsc , greater variability of R than H can only result from variability of Dsc in the opposite directions. An ordinary least squares regression of the month-to-month changes in foreign exchange reserves on the month-to-month changes in base money indicates no statistically significant relationship between them. The slope coefficient is negative with a P-Value of .23 ---indicating a 23 percent chance of observing a negative value of the magnitude observed purely on the basis of random chance when the true value is in fact zero---and the R-Square is only .01.