E-Liberary Pakistan: Triangle

This article is about the basic geometric shape. For other uses, see Triangle (disambiguation).

"Acute triangle" redirects here. For the trapezoid, see Isosceles trapezoid. For The Welcome to Paradox episode, see List of Welcome to Paradox episodes

Triangle
A triangle
Edges and vertices	3
Schläfli symbol	{3} (for equilateral)
Area	various methods; see below
Internal angle (degrees)	60° (for equilateral)

A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted

\triangle ABC

.
In Euclidean geometry any three points, when non-collinear, determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space).

Types of triangle

Euler diagram of types of triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. equilateral triangles are isosceles.

By relative lengths of sides

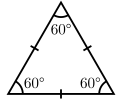
Triangles can be classified according to the relative lengths of their sides:

In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°.
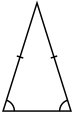
In an isosceles triangle, two sides are equal in length.An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the isosceles triangle theorem, which was known by Euclid. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides.The latter definition would make all equilateral triangles isosceles triangles. The 45–45–90 right triangle, which appears in the tetrakis square tiling, is isosceles.
In a scalene triangle, all sides are unequal, and equivalently all angles are unequal. A right triangle is also a scalene triangle if and only if it is not isosceles.


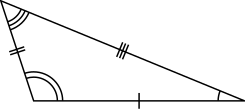Equilateral	Isosceles	Scalene

Hatch marks, also called tick marks, are used in diagrams of triangles and other geometric figures to identify sides of equal lengths. A side can be marked with a pattern of "ticks", short line segments in the form of tally marks; two sides have equal lengths if they are both marked with the same pattern. In a triangle, the pattern is usually no more than 3 ticks. An equilateral triangle has the same pattern on all 3 sides, an isosceles triangle has the same pattern on just 2 sides, and a scalene triangle has different patterns on all sides since no sides are equal. Similarly, patterns of 1, 2, or 3 concentric arcs inside the angles are used to indicate equal angles. An equilateral triangle has the same pattern on all 3 angles, an isosceles triangle has the same pattern on just 2 angles, and a scalene triangle has different patterns on all angles since no angles are equal.

Right triangles

The Pythagorean theorem

A central theorem is the Pythagorean theorem, which states in any right triangle, the square of the length of the hypotenuse equals the sum of the squares of the lengths of the two other sides. If the hypotenuse has length c, and the legs have lengths a and b, then the theorem states that

a^2 + b^2 = c^2.\,

The converse is true: if the lengths of the sides of a triangle satisfy the above equation, then the triangle has a right angle opposite side c.
Some other facts about right triangles:

The acute angles of a right triangle are complementary.

a + b + 90^{\circ} = 180^{\circ} \Rightarrow a + b = 90^{\circ} \Rightarrow a = 90^{\circ} - b

If the legs of a right triangle have the same length, then the angles opposite those legs have the same measure. Since these angles are complementary, it follows that each measures 45 degrees. By the Pythagorean theorem, the length of the hypotenuse is the length of a leg times √2.
In a right triangle with acute angles measuring 30 and 60 degrees, the hypotenuse is twice the length of the shorter side, and the longer side is equal to the length of the shorter side times √3:

c = 2a\,

b = a\times\sqrt{3}.

For all triangles, angles and sides are related by the law of cosines and law of sines (also called the cosine rule and sine rule).

Existence of a triangle

The triangle inequality states that the sum of the lengths of any two sides of a triangle must be greater than or equal to the length of the third side. That sum can equal the length of the third side only in the case of a degenerate triangle, one with collinear vertices. It is not possible for that sum to be less than the length of the third side.

Trigonometric conditions

Three positive angles α, β, and γ, each of them less than 180°, are the angles of a triangle if and only if any one of the following conditions holds:

\tan{\frac{\alpha}{2}}\tan{\frac{\beta}{2}}+\tan{\frac{\beta}{2}}\tan{\frac{\gamma}{2}}+\tan{\frac{\gamma}{2}}\tan{\frac{\alpha}{2}}=1,

\sin^2{\frac{\alpha}{2}}+\sin^2{\frac{\beta}{2}}+\sin^2{\frac{\gamma}{2}}+2\sin{\frac{\alpha}{2}}\sin{\frac{\beta}{2}}\sin{\frac{\gamma}{2}}=1.

Points, lines, and circles associated with a triangle

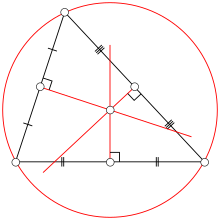
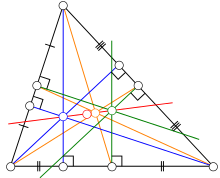
There are hundreds of different constructions that find a special point associated with (and often inside) a triangle, satisfying some unique property: see the references section for a catalogue of them. Often they are constructed by finding three lines associated in a symmetrical way with the three sides (or vertices) and then proving that the three lines meet in a single point: an important tool for proving the existence of these is Ceva's theorem, which gives a criterion for determining when three such lines are concurrent. Similarly, lines associated with a triangle are often constructed by proving that three symmetrically constructed points are collinear: here Menelaus' theorem gives a useful general criterion. In this section just a few of the most commonly encountered constructions are explained.

The circumcenter is the center of a circle passing through the three vertices of the triangle.

A perpendicular bisector of a side of a triangle is a straight line passing through the midpoint of the side and being perpendicular to it, i.e. forming a right angle with it. The three perpendicular bisectors meet in a single point, the triangle's circumcenter; this point is the center of the circumcircle, the circle passing through all three vertices. The diameter of this circle, called the circumdiameter, can be found from the law of sines stated above. The circumcircle's radius is called the circumradius.
Thales' theorem implies that if the circumcenter is located on one side of the triangle, then the opposite angle is a right one. If the circumcenter is located inside the triangle, then the triangle is acute; if the circumcenter is located outside the triangle, then the triangle is obtuse.

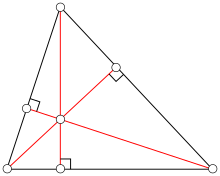
The intersection of the altitudes is the orthocenter.

An altitude of a triangle is a straight line through a vertex and perpendicular to (i.e. forming a right angle with) the opposite side. This opposite side is called the base of the altitude, and the point where the altitude intersects the base (or its extension) is called the foot of the altitude. The length of the altitude is the distance between the base and the vertex. The three altitudes intersect in a single point, called the orthocenter of the triangle. The orthocenter lies inside the triangle if and only if the triangle is acute.

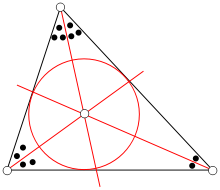
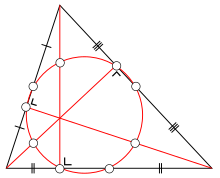
The intersection of the angle bisectors is the center of the incircle.

An angle bisector of a triangle is a straight line through a vertex which cuts the corresponding angle in half. The three angle bisectors intersect in a single point, the incenter, the center of the triangle's incircle. The incircle is the circle which lies inside the triangle and touches all three sides. Its radius is called the inradius. There are three other important circles, the excircles; they lie outside the triangle and touch one side as well as the extensions of the other two. The centers of the in- and excircles form an orthocentric system.

The intersection of the medians is the centroid.

A median of a triangle is a straight line through a vertex and the midpoint of the opposite side, and divides the triangle into two equal areas. The three medians intersect in a single point, the triangle's centroid or geometric barycenter. The centroid of a rigid triangular object (cut out of a thin sheet of uniform density) is also its center of mass: the object can be balanced on its centroid in a uniform gravitational field. The centroid cuts every median in the ratio 2:1, i.e. the distance between a vertex and the centroid is twice the distance between the centroid and the midpoint of the opposite side.

Nine-point circle demonstrates a symmetry where six points lie on the edge of the triangle.

The midpoints of the three sides and the feet of the three altitudes all lie on a single circle, the triangle's nine-point circle. The remaining three points for which it is named are the midpoints of the portion of altitude between the vertices and the orthocenter. The radius of the nine-point circle is half that of the circumcircle. It touches the incircle (at the Feuerbach point) and the three excircles.

Euler's line is a straight line through the centroid (orange), orthocenter (blue), circumcenter (green) and center of the nine-point circle (red).

The centroid (yellow), orthocenter (blue), circumcenter (green) and center of the nine-point circle (red point) all lie on a single line, known as Euler's line (red line). The center of the nine-point circle lies at the midpoint between the orthocenter and the circumcenter, and the distance between the centroid and the circumcenter is half that between the centroid and the orthocenter.
The center of the incircle is not in general located on Euler's line.
If one reflects a median in the angle bisector that passes through the same vertex, one obtains a symmedian. The three symmedians intersect in a single point, the symmedian point of the triangle.