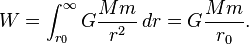E-Liberary Pakistan: Escape velocity

In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero.^{[nb 1]} It is the speed needed to "break free" from the gravitational attraction of a massive body, without further propulsion, i.e., without spending more fuel.
For a spherically symmetric body, the escape velocity at a given distance is calculated by the formula^[1]

v_e = \sqrt{\frac{2GM}{r}},

where G is the universal gravitational constant (G = 6.67×10⁻¹¹ m³ kg⁻¹ s⁻²), M the mass of the planet, star or other body, and r the distance from the center of gravity.^{[nb 2]}
In this equation atmospheric friction (air drag) is not taken into account. A rocket moving out of a gravity well does not actually need to attain escape velocity to do so, but could achieve the same result at any speed with a suitable mode of propulsion and sufficient fuel. Escape velocity only applies to ballistic trajectories.
The term escape velocity is actually a misnomer, and it is often more accurately referred to as escape speed since the necessary speed is a scalar quantity which is independent of direction (assuming a non-rotating planet and ignoring atmospheric friction or relativistic effects).

Overview
2 Orbit
3 List of escape velocities
4 Calculating an escape velocity
5 Deriving escape velocity using calculus
6 Multiple sources
7 See also
8 Notes
9 References

10 External links

Luna 1, launched in 1959, was the first man-made object to attain escape velocity from Earth

List of escape velocities

To leave planet Earth, an escape velocity of 11.2 km/s (approx. 40,320 km/h, or 25,000 mph) is required; however, a speed of 42.1 km/s is required to escape the Sun's gravity (and exit the Solar System) from the same position.

Location	with respect to	V_e (km/s)^[3]	Location	with respect to	V_e (km/s)^[3]
on the Sun,	the Sun's gravity:	617.5
on Mercury,	Mercury's gravity:	4.3^[4]^:230	at Mercury,	the Sun's gravity:	67.7
on Venus,	Venus's gravity:	10.3	at Venus,	the Sun's gravity:	49.5
on Earth,	Earth's gravity:	11.2^[4]^:200	at the Earth/Moon,	the Sun's gravity:	42.1
on the Moon,	the Moon's gravity:	2.4	at the Moon,	the Earth's gravity:	1.4
on Mars,	Mars' gravity:	5.0^[4]^:234	at Mars,	the Sun's gravity:	34.1
on Jupiter,	Jupiter's gravity:	59.6^[4]^:236	at Jupiter,	the Sun's gravity:	18.5
on Ganymede,	Ganymede's gravity:	2.7
on Saturn,	Saturn's gravity:	35.6^[4]^:238	at Saturn,	the Sun's gravity:	13.6
on Uranus,	Uranus' gravity:	21.3^[4]^:240	at Uranus,	the Sun's gravity:	9.6
on Neptune,	Neptune's gravity:	23.8^[4]^:240	at Neptune,	the Sun's gravity:	7.7
on Pluto,	Pluto's gravity:	1.2
at Solar System galactic radius,	the Milky Way's gravity:	492–594 ^[5]
on the event horizon,	a black hole's gravity:	≥ 299,792 (Speed of light)

Because of the atmosphere it is not useful and hardly possible to give an object near the surface of the Earth a speed of 11.2 km/s (40,320 km/h), as these speeds are too far in the hypersonic regime for most practical propulsion systems and would cause most objects to burn up due to aerodynamic heating or be torn apart by atmospheric drag. For an actual escape orbit a spacecraft is first placed in low Earth orbit (160–2,000 km) and then accelerated to the escape velocity at that altitude, which is a little less — about 10.9 km/s. The required change in speed, however, is far less because from a low Earth orbit the spacecraft already has a speed of approximately 8 km/s (28,800 km/h).

Calculating an escape velocity

To expand upon the derivation given in the Overview,

v_e = \sqrt{\frac{2GM}{r}} = \sqrt{\frac{2\mu}{r}} = \sqrt{2gr\,}

where

v_e

is the barycentric escape velocity, G is the gravitational constant, M is the mass of the body being escaped from, r is the distance between the center of the body and the point at which escape velocity is being calculated, g is the gravitational acceleration at that distance, and μ is the standard gravitational parameter.^[6]
The escape velocity at a given height is

\sqrt 2

times the speed in a circular orbit at the same height, (compare this with the velocity equation in circular orbit). This corresponds to the fact that the potential energy with respect to infinity of an object in such an orbit is minus two times its kinetic energy, while to escape the sum of potential and kinetic energy needs to be at least zero. The velocity corresponding to the circular orbit is sometimes called the first cosmic velocity, whereas in this context the escape velocity is referred to as the second cosmic velocity^[7]
For a body with a spherically-symmetric distribution of mass, the barycentric escape velocity

v_e

from the surface (in m/s) is approximately 2.364×10⁻⁵ m^1.5kg^−0.5s⁻¹ times the radius r (in meters) times the square root of the average density ρ (in kg/m³), or:

v_e \approx 2.364 \times 10^{-5} r \sqrt \rho.\,

Deriving escape velocity using calculus

Let G be the gravitational constant and let M be the mass of the earth (or other gravitating body) and m be the mass of the escaping body or projectile. At a distance r from the centre of gravitation the body feels an attractive force^[8]

F = G\frac{Mm}{r^2}.

The work needed to move the body over a small distance dr against this force is therefore given by

dW = G\frac{Mm}{r^2}\,dr.

The total work needed to move the body from the surface r₀ of the gravitating body to infinity is then

W = \int_{r_0}^{\infty} G\frac{Mm}{r^2}\,dr = G\frac{Mm}{r_0}.

This is the minimal required kinetic energy to be able to reach infinity, so the escape velocity v₀ satisfies

\tfrac{1}{2}m v_0^2 = G\frac{Mm}{r_0},

which results in

v_0 = \sqrt\frac{2GM}{r_0}.

Multiple sources

The escape velocity from a position in a field with multiple sources at rest with respect to each other is derived from the total potential energy per kg at that position, relative to infinity. The potential energies for all sources can simply be added. For the escape velocity it can be shown that this gives an escape velocity which is equal to the square root of the sum of the squares of the individual escape velocities due to each source.
For example, at the Earth's surface the escape velocity for the combination Earth and Sun would be

\scriptstyle\sqrt{11.2^2\ +\ 42.1^2}\ \mathrm{km}/\mathrm{s}=\ 43.56\ \mathrm{km}/\mathrm{s}