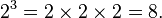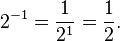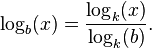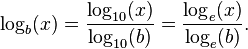Logarithm

In mathematics, the logarithm of a number is the exponent to which another fixed value, the base, must be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 10 to the power 3 is 1000: 1000 = 10 × 10 × 10 = 103. More generally, for any two real numbers b and x where b is positive and b ≠ 1,
y=b^x\Leftrightarrow x=\log_b(y)
The logarithm to base 10 (b = 10) is called the common logarithm and has many applications in science and engineering. The natural logarithm has the irrational (transcendental) number e (≈ 2.718) as its base; its use is widespread in pure mathematics, especially calculus. The binary logarithm uses base 2 (b = 2) and is prominent in computer science.

Logarithms were introduced by John Napier in the early 17th century as a means to simplify calculations. They were rapidly adopted by navigators, scientists, engineers, and others to perform computations more easily, using slide rules and logarithm tables. Tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition because of the fact—important in its own right—that the logarithm of a product is the sum of the logarithms of the factors:
\log_b(xy) = \log_b (x) + \log_b (y), \,
provided that b, x and y are all positive and b ≠ 1. The present-day notion of logarithms comes from Leonhard Euler, who connected them to the exponential function in the 18th century.
Logarithmic scales reduce wide-ranging quantities to smaller scopes. For example, the decibel is a logarithmic unit quantifying sound pressure and signal power ratios. In chemistry, pH is a logarithmic measure for the acidity of an aqueous solution. Logarithms are commonplace in scientific formulae, and in measurements of the complexity of algorithms and of geometric objects called fractals. They describe musical intervals, appear in formulae counting prime numbers, inform some models in psychophysics, and can aid in forensic accounting.

Graph showing a logarithm curves, which crosses the x-axis where x is 1 and extend towards minus infinity along the y-axis.
The graph of the logarithm to base 2 crosses the x axis (horizontal axis) at 1 and passes through the points with coordinates (2, 1), (4, 2), and (8, 3). For example, log2(8) = 3, because 23 = 8. The graph gets arbitrarily close to the y axis, but does not meet or intersect it.

In the same way as the logarithm reverses exponentiation, the complex logarithm is the inverse function of the exponential function applied to complex numbers. The discrete logarithm is another variant; it has applications in public-key cryptography.

Contents

  • 1 Motivation and definition
    • 1.1 Exponentiation
    • 1.2 Definition
    • 1.3 Examples
  • 2 Logarithmic identities
    • 2.1 Product, quotient, power and root
    • 2.2 Change of base

      Motivation and definition  The idea of logarithms is to reverse the operation of exponentiation, that is raising a number to a power. For example, the third power (or cube) of 2 is 8, because 8 is the product of three factors of 2:
      2^3 = 2 \times 2 \times 2 = 8. \,
      It follows that the logarithm of 8 with respect to base 2 is 3, so log2 8 = 3.

      Exponentiation

      The third power of some number b is the product of three factors of b. More generally, raising b to the n-th power, where n is a natural number, is done by multiplying n factors of b. The n-th power of b is written bn, so that
      b^n = \underbrace{b \times b \times \cdots \times b}_{n \text{ factors}}.
      Exponentiation may be extended to by, where b is a positive number and the exponent y is any real number. For example, b−1 is the reciprocal of b, that is, 1/b. (For further details, including the formula bm + n = bm · bn, see exponentiation or [1] for an elementary treatise.)

      Definition

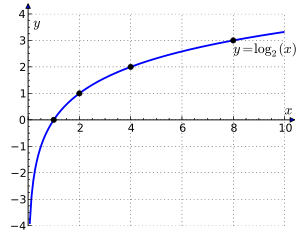
      The logarithm of a positive real number x with respect to base b, a positive real number not equal to 1[nb 1], is the exponent by which b must be raised to yield x. In other words, the logarithm of x to base b is the solution y to the equation[2]
      b^y = x. \,
      The logarithm is denoted "logb(x)" (pronounced as "the logarithm of x to base b" or "the base-b logarithm of x"). In the equation y = logb(x), the value y is the answer to the question "To what power must b be raised, in order to yield x?". This question can also be addressed (with a richer answer) for complex numbers, which is done in section "Complex logarithm", and this answer is much more extensively investigated in the page for the complex logarithm.

      Examples

      For example, log2(16) = 4, since 24 = 2 ×2 × 2 × 2 = 16. Logarithms can also be negative:
      \log_2 \!\left( \frac{1}{2} \right) = -1,\,
      since
      2^{-1} = \frac 1 {2^1} = \frac 1 2.
      A third example: log10(150) is approximately 2.176, which lies between 2 and 3, just as 150 lies between 102 = 100 and 103 = 1000. Finally, for any base b, logb(b) = 1 and logb(1) = 0, since b1 = b and b0 = 1, respectively.

      Logarithmic identities

      Main article: List of logarithmic identities
      Several important formulas, sometimes called logarithmic identities or log laws, relate logarithms to one another.[3]

      Product, quotient, power and root

      The logarithm of a product is the sum of the logarithms of the numbers being multiplied; the logarithm of the ratio of two numbers is the difference of the logarithms. The logarithm of the p-th power of a number is p times the logarithm of the number itself; the logarithm of a p-th root is the logarithm of the number divided by p. The following table lists these identities with examples. Each of the identities can be derived after substitution of the logarithm definitions x = blogb(x), and/or y = blogb(y), in the left hand sides.


      		 Formula Example
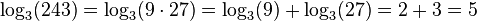
      product \log_b(x y) = \log_b (x) + \log_b (y) \, \log_3 (243) = \log_3(9 \cdot 27) = \log_3 (9) + \log_3 (27) = 2 + 3 = 5 \,
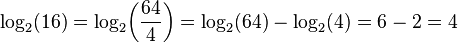
      quotient \log_b \!\left(\frac x y \right) = \log_b (x) - \log_b (y) \, \log_2 (16) = \log_2 \!\left ( \frac{64}{4} \right ) = \log_2 (64) - \log_2 (4) = 6 - 2 = 4
      power 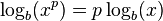\log_b(x^p) = p \log_b (x) \, \log_2 (64) = \log_2 (2^6) = 6 \log_2 (2) = 6 \,
      root \log_b \sqrt[p]{x} = \frac {\log_b (x)} p \, \log_{10} \sqrt{1000} = \frac{1}{2}\log_{10} 1000 = \frac{3}{2} = 1.5

      Change of base

      The logarithm logb(x) can be computed from the logarithms of x and b with respect to an arbitrary base k using the following formula:
      \log_b(x) = \frac{\log_k(x)}{\log_k(b)}.\,
      Typical scientific calculators calculate the logarithms to bases 10 and e.[4] Logarithms with respect to any base b can be determined using either of these two logarithms by the previous formula:
      \log_b (x) = \frac{\log_{10} (x)}{\log_{10} (b)} = \frac{\log_{e} (x)}{\log_{e} (b)}. \,
      Given a number x and its logarithm logb(x) to an unknown base b, the base is given by:
      b = x^\frac{1}{\log_b(x)}.
Labels: