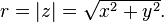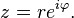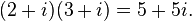A complex number can be visually represented as a pair of numbers (a, b) forming a vector on a diagram called an Argand diagram, representing the complex plane. "Re" is the real axis, "Im" is the imaginary axis, and i is the imaginary unit which satisfies the equation i2 = −1.
A complex number is a number of the form a + bi, where a and b are real numbers and i is an imaginary unit, satisfying i2 = −1. For example, −3.5 + 2i is a complex number.
The real number a is called the real part of the complex number a + bi; the real number b is called the imaginary part of a + bi. By this convention the imaginary part does not include the imaginary unit: hence b, not bi, is the imaginary part.The real part of a complex number z is denoted by Re(z) or ℜ(z); the imaginary part of a complex number z is denoted by Im(z) or ℑ(z). For example,
 . This expression is sometimes known as the Cartesian form of z.
. This expression is sometimes known as the Cartesian form of z.
A real number a can be regarded as a complex number a + 0i whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi whose real part is zero. It is common to write a for a + 0i and bi for 0 + bi. Moreover, when the imaginary part is negative, it is common to write a − bi with b > 0 instead of a + (−b)i, for example 3 − 4i instead of 3 + (−4)i.
The set of all complex numbers is denoted by ℂ, or
or  .
.
A complex number can be viewed as a point or position vector in a two-dimensional Cartesian coordinate system called the complex plane or Argand diagram (see Pedoe 1988 and Solomentsev 2001), named after Jean-Robert Argand.
The numbers are conventionally plotted using the real part as the
horizontal component, and imaginary part as vertical (see Figure 1).
These two values used to identify a given complex number are therefore
called its Cartesian, rectangular, or algebraic form.
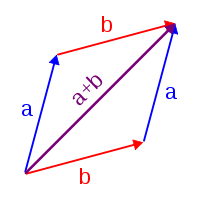
A position vector may also be defined in terms of its magnitude and direction relative to the origin. These are emphasized in a complex number's polar form. Using the polar form of the complex number in calculations may lead to a more intuitive interpretation of mathematical results. Notably, the operations of addition and multiplication take on a very natural geometric character when complex numbers are viewed as position vectors: addition corresponds to vector addition while multiplication corresponds to multiplying their magnitudes and adding their arguments (i.e. the angles they make with the x axis). Viewed in this way the multiplication of a complex number by i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin:
There is no linear ordering on the complex numbers that is compatible with addition and multiplication. Formally, we say that the complex numbers cannot have the structure of an ordered field. This is because any square in an ordered field is at least 0, but i2 = -1.
 or z*.
or z*.
Formally, for any complex number z:
 is the "reflection" of z about the real axis. In particular, conjugating twice gives the original complex number:
is the "reflection" of z about the real axis. In particular, conjugating twice gives the original complex number: 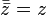 .
.
The real and imaginary parts of a complex number z can be extracted using the conjugate:
Conjugation distributes over the standard arithmetic operations:
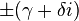 , where
, where
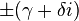 to obtain a + bi.Here
to obtain a + bi.Here 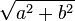 is called the modulus of a + bi, and the square root with non-negative real part is called the principal square root; also
is called the modulus of a + bi, and the square root with non-negative real part is called the principal square root; also  , where
, where  .
.
The absolute value (or modulus or magnitude) of a complex number z = x + yi is
 is the complex conjugate of
is the complex conjugate of  .
.
The argument of z (in many applications referred to as the "phase") is the angle of the radius OP with the positive real axis, and is written as . As with the modulus, the argument can be found from the rectangular form
. As with the modulus, the argument can be found from the rectangular form  :
:
The value of φ equals the result of atan2: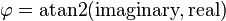 .
.
Together, r and φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called trigonometric form
Formulas for multiplication, division and exponentiation are simpler
in polar form than the corresponding formulas in Cartesian coordinates.
Given two complex numbers z1 = r1(cos φ1 + i sin φ1) and z2 = r2(cos φ2 + i sin φ2), because of the well-known trigonometric identities
Similarly, division is given by
Definition
The real number a is called the real part of the complex number a + bi; the real number b is called the imaginary part of a + bi. By this convention the imaginary part does not include the imaginary unit: hence b, not bi, is the imaginary part.The real part of a complex number z is denoted by Re(z) or ℜ(z); the imaginary part of a complex number z is denoted by Im(z) or ℑ(z). For example,
 . This expression is sometimes known as the Cartesian form of z.
. This expression is sometimes known as the Cartesian form of z.A real number a can be regarded as a complex number a + 0i whose imaginary part is 0. A purely imaginary number bi is a complex number 0 + bi whose real part is zero. It is common to write a for a + 0i and bi for 0 + bi. Moreover, when the imaginary part is negative, it is common to write a − bi with b > 0 instead of a + (−b)i, for example 3 − 4i instead of 3 + (−4)i.
The set of all complex numbers is denoted by ℂ,
 or
or  .
.Notation
Some authors write a + ib instead of a + bi. In some disciplines, in particular electromagnetism and electrical engineering, j is used instead of i, since i is frequently used for electric current. In these cases complex numbers are written as a + bj or a + jb.Complex plane
Main article: Complex plane
A position vector may also be defined in terms of its magnitude and direction relative to the origin. These are emphasized in a complex number's polar form. Using the polar form of the complex number in calculations may lead to a more intuitive interpretation of mathematical results. Notably, the operations of addition and multiplication take on a very natural geometric character when complex numbers are viewed as position vectors: addition corresponds to vector addition while multiplication corresponds to multiplying their magnitudes and adding their arguments (i.e. the angles they make with the x axis). Viewed in this way the multiplication of a complex number by i corresponds to rotating the position vector counterclockwise by a quarter turn (90°) about the origin:

Relations
Equality
Two complex numbers are equal if and only if both their real and imaginary parts are equal. In symbols:Ordering
Because complex numbers are naturally thought of as existing on a two-dimensional plane, there is no natural linear ordering on the set of complex numbers.There is no linear ordering on the complex numbers that is compatible with addition and multiplication. Formally, we say that the complex numbers cannot have the structure of an ordered field. This is because any square in an ordered field is at least 0, but i2 = -1.
Elementary operations
Conjugation
Main article: Complex conjugate
The complex conjugate of the complex number z = x + yi is defined to be x − yi. It is denoted  or z*.
or z*.Formally, for any complex number z:
 is the "reflection" of z about the real axis. In particular, conjugating twice gives the original complex number:
is the "reflection" of z about the real axis. In particular, conjugating twice gives the original complex number: 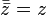 .
.The real and imaginary parts of a complex number z can be extracted using the conjugate:
Conjugation distributes over the standard arithmetic operations:
Addition and subtraction
Complex numbers are added by adding the real and imaginary parts of the summands. That is to say:Multiplication and division
The multiplication of two complex numbers is defined by the following formula: (distributive law)
(distributive law)
-
 (commutative law of addition—the order of the summands can be changed)
(commutative law of addition—the order of the summands can be changed) (commutative and distributive laws)
(commutative and distributive laws) (fundamental property of the imaginary unit).
(fundamental property of the imaginary unit).
-
Square root
See also: Square roots of negative and complex numbers
The square roots of a + bi (with b ≠ 0) are 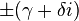 , where
, where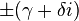 to obtain a + bi.Here
to obtain a + bi.Here 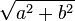 is called the modulus of a + bi, and the square root with non-negative real part is called the principal square root; also
is called the modulus of a + bi, and the square root with non-negative real part is called the principal square root; also  , where
, where  .
.Polar form
Main article: Polar coordinate system
Absolute value and argument
An alternative way of defining a point P in the complex plane, other than using the x- and y-coordinates, is to use the distance of the point from O, the point whose coordinates are (0, 0) (the origin), together with the angle subtended between the positive real axis and the line segment OP in a counterclockwise direction. This idea leads to the polar form of complex numbers.The absolute value (or modulus or magnitude) of a complex number z = x + yi is
 is the complex conjugate of
is the complex conjugate of  .
.The argument of z (in many applications referred to as the "phase") is the angle of the radius OP with the positive real axis, and is written as
 . As with the modulus, the argument can be found from the rectangular form
. As with the modulus, the argument can be found from the rectangular form  :
:The value of φ equals the result of atan2:
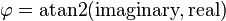 .
.Together, r and φ give another way of representing complex numbers, the polar form, as the combination of modulus and argument fully specify the position of a point on the plane. Recovering the original rectangular co-ordinates from the polar form is done by the formula called trigonometric form
Multiplication and division in polar form
Similarly, division is given by



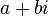 is the rectangular expression of the point.
is the rectangular expression of the point.




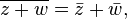
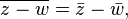





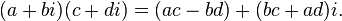






 or
or 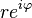 are polar expressions of the point.
are polar expressions of the point.