Inflection point

In differential calculus, an inflection point, point of inflection, flex, or inflection (inflexion) is a point on a curve at which the curvature or concavity changes sign from plus to minus or from minus to plus. The curve changes from being concave (positive curvature) to convex (negative curvature), or vice versa.
A point where the curvature vanishes but does not change sign is sometimes called a point of undulation or undulation point.
In algebraic geometry an inflection point is defined slightly more generally, as a point where the tangent meets the curve to order at least 3, and an undulation point or hyperflex is defined as a point where the tangent meets the curve to order at least 4.

Plot of y = x³ with inflection point of (0,0), also a saddle point.

Contents

• 1 Equivalent forms
• 2 A necessary but not sufficient condition
• 3 Categorization of points of inflection
• 4 Functions with discontinuitie

Graph showing the relationship between the roots, turning points, stationary points, inflection point and concavity of a cubic polynomial x³ - 3x² - 144x + 432 and its first and second derivatives.

In differential calculus, an inflection point, point of inflection, flex, or inflection

Equivalent forms

The following are all equivalent to the above definition:

• a point on a curve at which the second derivative changes sign. This is very similar to the previous definition, since the sign of the curvature is always the same as the sign of the second derivative, but note that the curvature is not the same as the second derivative.
• a point (x, y) on a function, f(x), at which the first derivative, f′(x), is at an extremum, i.e. a (local) minimum or maximum. (This is not the same as saying that y is at an extremum).
• a point p on a curve at which the tangent crosses the curve at that point. For an algebraic curve, this means a non singular point where the multiplicity of the intersection at p of the tangent line and the curve is odd and greater than 2.^[2]

Plot of f(x) = sin(2x) from −π/4 to 5π/4; note f’s second derivative is f″(x) = –4sin(2x). Tangent is blue where the curve is concave (above its own tangent), green where convex (below its tangent), and red at inflection points: 0, π/2 and π

A necessary but not sufficient condition

If x is an inflection point for f then the second derivative, f″(x), is equal to zero if it exists, but this condition does not provide a sufficient definition of a point of inflection. One also needs the lowest-order (above the second) non-zero derivative to be of odd order (third, fifth, etc.). If the lowest-order non-zero derivative is of even order, the point is not a point of inflection, but an undulation point. However, in algebraic geometry, both inflection points and undulation points are usually called inflection points. An example of such an undulation point is y = x⁴ for x=0.
It follows from the definition that the sign of f′(x) on either side of the point (x,y) must be the same. If this is positive, the point is a rising point of inflection; if it is negative, the point is a falling point of inflection.

Categorization of points of inflection

Points of inflection can also be categorized according to whether f′(x) is zero or not zero.

• if f′(x) is zero, the point is a stationary point of inflection, also known as a saddle-point
• if f′(x) is not zero, the point is a non-stationary point of inflection

y = x⁴ – x has a 2nd derivative of zero at point (0,0), but it is not an inflection point because the fourth derivative is the first higher order non-zero derivative (the third derivative is zero as well).

An example of a saddle point is the point (0,0) on the graph y = x³. The tangent is the x-axis, which cuts the graph at this point.
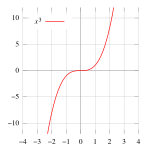
A non-stationary point of inflection can be visualised if the graph y = x³ is rotated slightly about the origin. The tangent at the origin still cuts the graph in two, but its gradient is non-zero.
Note that an inflection point is also called an ogee, although this term is sometimes applied to the entire curve which contains an inflection point.^{[citation needed]}

Functions with discontinuities

Some functions change concavity without having points of inflection. Instead, they can change concavity around vertical asymptotes or discontinuities. Take, for example, the function 2x²/(x² – 1). It is concave when |x| > 1 and convex when |x| < 1. However, it has no points of inflection because 1 and -1 are not in the domain of the function.