- First law: When viewed in an inertial reference frame, an object either remains at rest or continues to move at a constant velocity, unless acted upon by an external force.
- Second law: F = ma. The vector sum of the forces F on an object is equal to the mass m of that object multiplied by the acceleration vector a of the object.
- Third law: When one body exerts a force on a second body, the second body simultaneously exerts a force equal in magnitude and opposite in direction on the first body.
Contents
- 1 Overview
- 2 Newton's first law
- 3 Newton's second law
- 3.1 Impulse
- 3.2 Variable-mass systems
- 4 Newton's third law
- 5 History
- 5.1 Newton's 1st Law
- 5.2 Newton's 2nd Law
- 5.3 Newton's 3rd LawNewton's laws are applied to objects which are idealised as single point masses,in the sense that the size and shape of the object's body are neglected
to focus on its motion more easily. This can be done when the object is
small compared to the distances involved in its analysis, or the deformation
and rotation of the body are of no importance. In this way, even a
planet can be idealised as a particle for analysis of its orbital motion
around a star.
In their original form, Newton's laws of motion are not adequate to characterise the motion of rigid bodies and deformable bodies. Leonhard Euler in 1750 introduced a generalisation of Newton's laws of motion for rigid bodies called the Euler's laws of motion, later applied as well for deformable bodies assumed as a continuum. If a body is represented as an assemblage of discrete particles, each governed by Newton's laws of motion, then Euler's laws can be derived from Newton's laws. Euler's laws can, however, be taken as axioms describing the laws of motion for extended bodies, independently of any particle structure.
Newton's first law
The first law states that if the net force (the vector sum of all forces acting on an object) is zero, then the velocity of the object is constant. Velocity is a vector quantity which expresses both the object's speed and the direction of its motion; therefore, the statement that the object's velocity is constant is a statement that both its speed and the direction of its motion are constant. The first law can be stated mathematically as
- An object that is at rest will stay at rest unless an external force acts upon it.
- An object that is in motion will not change its velocity unless an external force acts upon it.
Newton's second law
The second law states that the net force on an object is equal to the rate of change (that is, the derivative) of its linear momentum p in an inertial reference frame:
Consistent with the first law, the time derivative of the momentum is non-zero when the momentum changes direction, even if there is no change in its magnitude; such is the case with uniform circular motion. The relationship also implies the conservation of momentum: when the net force on the body is zero, the momentum of the body is constant. Any net force is equal to the rate of change of the momentum.
Any mass that is gained or lost by the system will cause a change in momentum that is not the result of an external force. A different equation is necessary for variable-mass systems.
Newton's second law requires modification if the effects of special relativity are to be taken into account, because at high speeds the approximation that momentum is the product of rest mass and velocity is not accurate.
Impulse
An impulse J occurs when a force F acts over an interval of time Δt, and it is given by
Impulse is a concept frequently used in the analysis of collisions and impacts.
Variable-mass systems
Main article: Variable-mass systemVariable-mass systems, like a rocket burning fuel and ejecting spent gases, are not closed and cannot be directly treated by making mass a function of time in the second law; that is, the following formula is wrong:
Newton's third law
The third law states that all forces exist in pairs: if one object A exerts a force FA on a second object B, then B simultaneously exerts a force FB on A, and the two forces are equal and opposite: FA = −FB. The third law means that all forces are interactions between different bodies, and thus that there is no such thing as a unidirectional force or a force that acts on only one body. This law is sometimes referred to as the action-reaction law, with FA called the "action" and FB the "reaction". The action and the reaction are simultaneous, and it does not matter which is called the action and which is called reaction; both forces are part of a single interaction, and neither force exists without the other.
The two forces in Newton's third law are of the same type (e.g., if the road exerts a forward frictional force on an accelerating car's tires, then it is also a frictional force that Newton's third law predicts for the tires pushing backward on the road).
From a conceptual standpoint, Newton's third law is seen when a person walks: they push against the floor, and the floor pushes against the person. Similarly, the tires of a car push against the road while the road pushes back on the tires—the tires and road simultaneously push against each other. In swimming, a person interacts with the water, pushing the water backward, while the water simultaneously pushes the person forward—both the person and the water push against each other. The reaction forces account for the motion in these examples. These forces depend on friction; a person or car on ice, for example, may be unable to exert the action force to produce the needed reaction force. 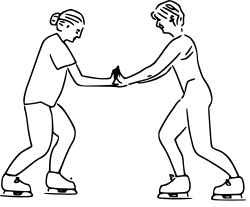 An illustration of Newton's third law in which two skaters push against each other. The first skater on the left exerts a normal force N12 on the second skater directed towards the right, and the second skater exerts a normal force N21 on the first skater directed towards the left.
An illustration of Newton's third law in which two skaters push against each other. The first skater on the left exerts a normal force N12 on the second skater directed towards the right, and the second skater exerts a normal force N21 on the first skater directed towards the left.
The magnitude of both forces are equal, but they have opposite directions, as dictated by Newton's third law.


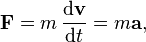


![\mathbf{F}_\mathrm{net} = \frac{\mathrm{d}}{\mathrm{d}t}\big[m(t)\mathbf{v}(t)\big] = m(t) \frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t} + \mathbf{v}(t) \frac{\mathrm{d}m}{\mathrm{d}t}. \qquad \mathrm{(wrong)}](http://upload.wikimedia.org/math/4/5/f/45f0d6b5ec0038d6bad24d85274e027c.png)
