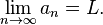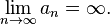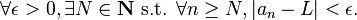Sequence

"Sequential" redirects here. For the manual transmission, see Sequential manual transmission. For other uses, see Sequence (disambiguation).
A sequence is an ordered list. Like a set, it contains members (also called elements, or terms). The number of ordered elements (possibly infinite) is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence. Most precisely, a sequence can be defined as a function whose domain is a countable totally ordered set, such as the natural numbers.
For example, (M, A, R, Y) is a sequence of letters with the letter 'M' first and 'Y' last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be finite, as in this example, or infinite, such as the sequence of all even positive integers (2, 4, 6,...). Finite sequences are sometimes known as strings or words and infinite sequences as streams. The empty sequence ( ) is included in most notions of sequence, but may be excluded depending on the context.

An infinite sequence of real numbers (in blue). This sequence is neither increasing, nor decreasing, nor convergent, nor Cauchy. It is, however, bounded.

Contents

  • 1 Examples and notation
    • 1.1 Important examples
    • 1.2 Indexing
    • 1.3 Specifying a sequence by recursion
      • 3 Limits and convergence
        • 3.1 Definition of convergence
        • 3.2 Applications and important results
        • 3.3 Cauchy sequences
      • 4 Series

      Examples and notation

      A sequence can be thought of as a list of elements with a particular order. Sequences are useful in a number of mathematical disciplines for studying functions, spaces, and other mathematical structures using the convergence properties of sequences. In particular, sequences are the basis for series, which are important in differential equations and analysis. Sequences are also of interest in their own right and can be studied as patterns or puzzles, such as in the study of prime numbers.
      There are a number of ways to denote a sequence, some of which are more useful for specific types of sequences. One way to specify a sequence is to list the elements. For example, the first four odd numbers form the sequence (1,3,5,7). This notation can be used for infinite sequences as well. For instance, the infinite sequence of positive odd integers can be written (1,3,5,7,...). Listing is most useful for infinite sequences with a pattern that can be easily discerned from the first few elements. Other ways to denote a sequence are discussed after the examples.

      Important examples

      A tiling with squares whose sides are successive Fibonacci numbers in length.
      There are many important integer sequences. The prime numbers are the natural numbers bigger than 1, that have no divisors but 1 and themselves. Taking these in their natural order gives the sequence (2,3,5,7,11,13,17,...). The study of prime numbers has important applications for mathematics and specifically number theory.
      The Fibonacci numbers are the integer sequence whose elements are the sum of the previous two elements. The first two elements are either 0 and 1 or 1 and 1 so that the sequence is (0,1,1,2,3,5,8,13,21,34,...).
      Other interesting sequences include the ban numbers, whose spellings do not contain a certain letter of the alphabet. For instance, the eban numbers (do not contain 'e') form the sequence (2,4,6,30,32,34,36,40,42,...). Another sequence based on the English spelling of the letters is the one based on their number of letters (3,3,5,4,4,3,5,5,4,3,6,6,8,...).
      For a list of important examples of integers sequences see On-line Encyclopedia of Integer Sequences.
      Other important examples of sequences include ones made up of rational numbers, real numbers, and complex numbers. The sequence (.9,.99,.999,.9999,...) approaches the number 1. In fact, every real number can be written as the limit of a sequence of rational numbers. For instance, for a sequence (3,3.1,3.14,3.141,3.1415,...) the limit of a sequence can be written as π. It is this fact that allows us to write any real number as the limit of a sequence of decimals. The decimal for π, however, does not have any pattern like the one for the sequence (0.9,0.99,...).

      Indexing

      Other notations can be useful for sequences whose pattern cannot be easily guessed, or for sequences that do not have a pattern such as the digits of π. This section focuses on the notations used for sequences that are a map from a subset of the natural numbers. For generalizations to other countable index sets see the following section and below.
      The terms of a sequence are commonly denoted by a single variable, say an, where the index n indicates the nth element of the sequence.
      \begin{align} a_1 &\leftrightarrow& \text{ 1st element} \\ a_2 &\leftrightarrow &\text{ 2nd element } \\ a_3 &\leftrightarrow &\text{ 3rd element } \\ \vdots& &\vdots \\ a_{n-1} &\leftrightarrow &\text{ (n-1)th element} \\ a_n &\leftrightarrow &\text{ nth element} \\ a_{n+1} &\leftrightarrow &\text{ (n+1)th element} \\ \vdots& &\vdots \end{align}
      Indexing notation is used to refer to a sequence in the abstract. It is also a natural notation for sequences whose elements are related to the index n (the element's position) in a simple way. For instance, the sequence of the first 10 square numbers could be written as
      (a_1,a_2,...,a_{10}), \qquad a_k = k^2.
      This represents the sequence (1,4,9,...100). This notation is often simplified further as
      (a_k)_{k=1}^{10}, \qquad a_k = k^2.
      Here the subscript {k=1} and superscript 10 together tell us that the elements of this sequence are the ak such that k = 1, 2, ..., 10.
      Sequences can be indexed beginning and ending from any integer. The infinity symbol ∞ is often used as the superscript to indicate the sequence including all integer k-values starting with a certain one. The sequence of all positive squares is then denoted
      (a_k)_{k=1}^\infty, \qquad a_k = k^2.
      In cases where the set of indexing numbers is understood, such as in analysis, the subscripts and superscripts are often left off. That is, one simply writes ak for an arbitrary sequence. In analysis, k would be understood to run from 1 to ∞. However, sequences are often indexed starting from zero, as in
      (a_k)_{k=0}^\infty = ( a_0, a_1, a_2,... ).
      In some cases the elements of the sequence are related naturally to a sequence of integers whose pattern can be easily inferred. In these cases the index set may be implied by a listing of the first few abstract elements. For instance, the sequence of squares of odd numbers could be denoted in any of the following ways.
    • (1,9,25,...)
    • (a_1,a_3,a_5,...), \qquad a_k = k^2
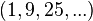
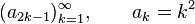
    • (a_{2k-1})_{k=1}^\infty, \qquad a_k = k^2
    • (a_{k})_{k=1}^\infty, \qquad a_k = (2k-1)^2
    • ((2k-1)^2)_{k=1}^\infty
    Moreover, the subscripts and superscripts could have been left off in the third, fourth, and fifth notations if the indexing set was understood to be the natural numbers.
    Finally, sequences can more generally be denoted by writing a set inclusion in the subscript, such as in
    (a_k)_{k \in \mathbf{N}}
    The set of values that the index can take on is called the index set. In general, the ordering of the elements ak is specified by the order of the elements in the indexing set. When N is the index set, the element ak+1 comes after the element ak since in N, the element (k+1) comes directly after the element k.

    Specifying a sequence by recursion

    Sequences whose elements are related to the previous elements in a straightforward way are often specified using recursion. This is in contrast to the specification of sequence elements in terms of their position.
    To specify a sequence by recursion requires a rule to construct each consecutive element in terms of the ones before it. In addition, enough initial elements must be specified so that new elements of the sequence can be specified by the rule. The principle of mathematical induction can be used to prove that a sequence is well-defined, which is to say that that every element of the sequence is specified at least once and has a single, unambiguous value. Induction can also be used to prove properties about a sequence, especially for sequences whose most natural specification is by recursion.
    The Fibonacci sequence can be defined using a recursive rule along with two initial elements. The rule is that each element is the sum of the previous two elements, and the first two elements are 0 and 1.
    a_n = a_{n-1} + a_{n-2},   with   a0 = 0  and  a1 = 1.
    The first ten terms of this sequence are 0,1,1,2,3,5,8,13,21, and 34. A more complicated example of a sequence that is defined recursively is Recaman's sequence, considered at the beginning of this section. We can define Recaman's sequence by
    a0 = 0  and  an = an−1−n   if the result is positive and not already in the list. Otherwise,   an = an−1+n .
    Not all sequences can be specified by a rule in the form of an equation, recursive or not, and some can be quite complicated. For example, the sequence of prime numbers is the set of prime numbers in their natural order. This gives the sequence (2,3,5,7,11,13,17,...).

    Limits and convergence

    Main article: Limit of a sequence
    The plot of a convergent sequence (an) is shown in blue. Visually we can see that the sequence is converging to the limit zero as n increases.
    One of the most important properties of a sequence is convergence. Informally, a sequence converges if it has a limit. Continuing informally, a (singly infinite) sequence has a limit if it approaches some value L, called the limit, as n becomes very large. That is, for an abstract sequence (an) (with n running from 1 to infinity understood) the value of an approaches L as n → ∞, denoted
    \lim_{n\to\infty} a_n = L.
    More precisely, the sequence converges if there exists a limit L such that the remaining an's are arbitrarily close to L for some n large enough.
    If a sequence converges to some limit, then it is convergent; otherwise it is divergent.
    If an gets arbitrarily large as n → ∞ we write
    \lim_{n\to\infty}a_n = \infty.
    In this case the sequence (an) diverges, or that it converges to infinity.
    If an becomes arbitrarily "small" negative numbers (large in magnitude) as n → ∞ we write
    \lim_{n\to\infty}a_n = -\infty
    and say that the sequence diverges or converges to minus infinity.

    Definition of convergence

    For sequences that can be written as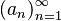 (a_n)_{n=1}^\infty with an ∈ R we can write (an) with the indexing set understood as N. These sequences are most common in real analysis. The generalizations to other types of sequences are considered in the following section and the main page Limit of a sequence.
    Let (an) be a sequence. In words, the sequence (an) is said to converge if there exists a number L such that no matter how close we want the an to be to L (say ε-close where ε > 0), we can find a natural number N such that all terms (aN+1, aN+2, ...) are further closer to L (within ε of L). This is often written more compactly using symbols. For instance,
    for all ε > 0, there exists a natural number N such that L−ε < an < L+ε for all n ≥ N.
    In even more compact notation
    \forall \epsilon > 0, \exists N \in \mathbf{N} \text{ s.t. } \forall n\geq N, |a_n-L|<\epsilon.
    The difference in the definitions of convergence for (one-sided) sequences in complex analysis and metric spaces is that the absolute value |an − L| is interpreted as the distance in the complex plane (\sqrt{z^*z}), and the distance under the appropriate metric, respectively.

    Applications and important results

    Important results for convergence and limits of (one-sided) sequences of real numbers include the following. These equalities are all true at least when both sides exist. For a discussion of when the existence of the limit on one side implies the existence of the other see a real analysis text such as can be found in the references.
  • The limit of a sequence is unique.
  • \lim_{n\to\infty} (a_n \pm b_n) = \lim_{n\to\infty} a_n \pm \lim_{n\to\infty} b_n
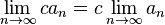
  • \lim_{n\to\infty} c a_n = c \lim_{n\to\infty} a_n
  • \lim_{n\to\infty} (a_n b_n) = (\lim_{n\to\infty} a_n)( \lim_{n\to\infty} b_n)
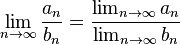  • \lim_{n\to\infty} \frac{a_n} {b_n} = \frac{ \lim_{n\to\infty} a_n}{ \lim_{n\to\infty} b_n} provided \lim_{n\to\infty} b_n \ne 0
  • \lim_{n\to\infty} a_n^p = \left[ \lim_{n\to\infty} a_n \right]^p
  • If an ≤ bn for all n greater than some N, then \lim_{n\to\infty} a_n \leq \lim_{n\to\infty} b_n .
  • (Squeeze Theorem) If a_n \leq c_n \leq b_n for all n > N, and \lim_{n\to\infty} a_n = \lim_{n\to\infty} b_n = L,   then \lim_{n\to\infty} c_n = L.
  • If a sequence is bounded and monotonic then it is convergent.
  • A sequence is convergent if and only if every subsequence is convergent.

Cauchy sequences

Main article: Cauchy sequence
The plot of a Cauchy sequence (Xn), shown in blue, as Xn versus n. Visually, we see that the sequence appears to be converging to the limit zero as the terms in the sequence become closer together as n increases. In the real numbers every Cauchy sequence converges to some limit.
A Cauchy sequence is a sequence whose terms become arbitrarily close together as n gets very large. The notion of a Cauchy sequence is important in the study of sequences in metric spaces, and, in particular, in real analysis. One particularly important result in real analysis is Cauchy characterization of convergence for sequences:
In the real numbers, a sequence is convergent if and only if it is Cauchy.
In contrast, in the rational numbers, e.g. the sequence defined by x1 = 1 and xn+1 = xn + 2/xn/2 is Cauchy, but has no rational limit, cf. here.

Series

Main article: Series (mathematics)
A series is, informally speaking, the sum of the terms of a sequence. That is, adding the first N terms of a (one-sided) sequence forms the Nth term of another sequence, called a series. Thus the N series of the sequence (an) results in another sequence (SN) given by:
\begin{align} S_1 &=& a_1& & &\\ S_2 &=& a_1& {}+ a_2& &\\ S_3 &= &a_1& {}+ a_2& {}+ a_3&\\ \vdots & &\vdots & & &\\ S_N &=& a_1& {}+ a_2& {}+ a_3& {}+ \cdots \\ \vdots & &\vdots & & &\end{align}
We can also write the nth term of the series as
S_N = \sum_{n=1}^N a_n.
Then the concepts used to talk about sequences, such as convergence, carry over to series (the sequence of partial sums) and the properties can be characterized as properties of the underlying sequences (such as (an) in the last example). The limit, if it exists, of an infinite series (the series created from an infinite sequence) is written as
\lim_{N\to\infty}S_N = \sum_{n=1}^{\infty} a_n.
Labels: