| (i) | ||||
| (ii) | ||||
| (iii) | ||||
| (iv) |
How to determine if a stationary point is a max, min or point of inflection.
The rate of change of the slope either side of a turning point reveals its type.
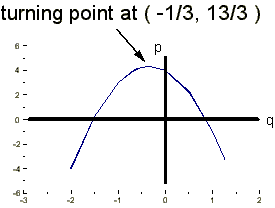
But a rate of change is a differential. So all we need to do is differentiate the slope, dy/dx, with respect to x. In other words we need the 2nd differential, or
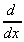 (dy/dx), more usually called
(dy/dx), more usually called 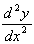 (dee 2 y by dee x squared)
(dee 2 y by dee x squared)Examples
1. y(x) = 9x2 - 2
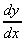 = 18x
= 18x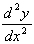 = 18
= 182. y(x) = 4x5 -
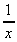
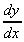 = 20x4 +
= 20x4 +
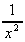
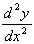 = 80x3 -
= 80x3 -
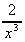
3. p = 3q3 - 4q2 + 6
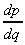 = 9q2 -
8q
= 9q2 -
8q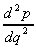 = 18q - 8
= 18q - 8Rules for stationary points
i) At a local maximum,
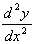 = -ve
= -ve
ii) At a local minimum,
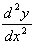 = +ve
= +ve
iii) At a point of inflexion,
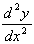 = 0, and we must examine the gradient either side of
the turning point to find out if the curve is a +ve or
-ve p.o.i.
= 0, and we must examine the gradient either side of
the turning point to find out if the curve is a +ve or
-ve p.o.i.Examples
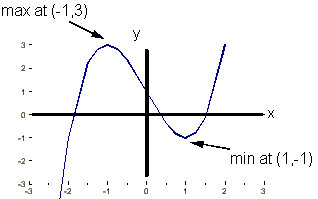
1. Taking the same example as we used before:
y(x) = x3 - 3x + 1
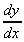 = 3x2 -
3, giving stationary points at (-1,3) and (1,-1)
= 3x2 -
3, giving stationary points at (-1,3) and (1,-1)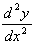 = 6x
= 6xAt stationary point (-1,3), x = -1, so
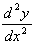 = -6, so it's a maximum.
= -6, so it's a maximum.At stationary point (1,-1), x = +1, so
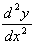 = +6, so it's a minimum
= +6, so it's a minimumSo we can finally sketch the curve:
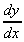 = 3x2, which
is equal to zero at the stationary point.
= 3x2, which
is equal to zero at the stationary point.If 3x2 = 0, x = 0, and so y = +8, so the stationary point is at (0,8).
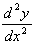 = 6x
= 6x So, at the stationary point (0,8),
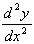 =
0, so we have a point of inflexion. But dy/dx is +ve either
side of this point (e.g. at x = +1, dy/dx
= +3, at x = -1, dy/dx = +3), so the curve has a
positive point of inflection.
=
0, so we have a point of inflexion. But dy/dx is +ve either
side of this point (e.g. at x = +1, dy/dx
= +3, at x = -1, dy/dx = +3), so the curve has a
positive point of inflection.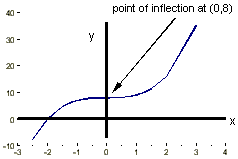
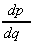 = -2 - 6q, which at the turning
point = 0
= -2 - 6q, which at the turning
point = 0
so -2 - 6q = 0, 6q = -2, q = -
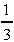 ,
and p = 4
,
and p = 4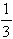
We have one turning point at (-
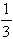 ,
4
,
4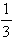 ).
).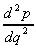 = -6, so the turning point is a maximum.
= -6, so the turning point is a maximum.
(This is consistent with what we said earlier, that for quadratics if the x2 term is -ve, we have a maximum).
More complicated Differentiation Rules
A. Product Rule
If a function y(x) can be written as the product of two other functions, say u(x) and v(x), then the differential of y(x) is given by the product rule:
then
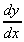 = u.
= u.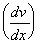 +
v.
+
v.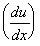
Examples
1. y(x) = (x2 + 2)(x + 1)
let u = x2 + 2, so that du/dx = 2x
let v = x + 1, so that dv/dx = 1
so
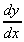 = u.
= u.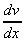 + v
+ v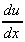 = (x2 +
2).1 + (x + 1).2x
= (x2 +
2).1 + (x + 1).2x= 3x2 + 2x + 2
(Note: we can check this by expanding out the brackets)
y(x) = x3 + x2 + 2x + 1, dy/dx = 3x2 + 2x + 2
2. y(x) = x3(3 -
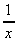 + 3x2)
+ 3x2)
Let u = x3, and v = 3 -
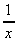 + 3x2
+ 3x2
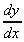 = x3(
= x3(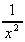 + 6x) + (3 -
+ 6x) + (3 - 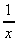 + 3x2).3x2
+ 3x2).3x2