E-Liberary Pakistan: DIFFERENTIATION USING THE CHAIN RULE

The following problems require the use of the chain rule. The chain rule is a rule for differentiating compositions of functions. In the following discussion and solutions the derivative of a function h(x) will be denoted by $tex2html_wrap_inline53$ or h'(x) . Most problems are average. A few are somewhat challenging. The chain rule states formally that

$tex2html_wrap_inline57$ .

However, we rarely use this formal approach when applying the chain rule to specific problems. Instead, we invoke an intuitive approach. For example, it is sometimes easier to think of the functions f and g as ``layers'' of a problem. Function f is the ``outer layer'' and function g is the ``inner layer.'' Thus, the chain rule tells us to first differentiate the outer layer, leaving the inner layer unchanged (the term f'( g(x) ) ) , then differentiate the inner layer (the termg'(x) ) . This process will become clearer as you do the problems. In most cases, final answers are given in the most simplified form.

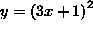
PROBLEM 1 : Differentiate $tex2html_wrap_inline71$
SOLUTION 1 : Differentiate 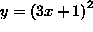$tex2html_wrap_inline528$ .( The outer layer is ``the square'' and the inner layer is (3x+1) . Differentiate ``the square'' first, leaving (3x+1) unchanged. Then differentiate (3x+1). ) Thus,

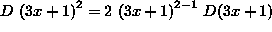$tex2html_wrap_inline536$

= 2 (3x+1) (3)

= 6 (3x+1) .

PROBLEM 2 : Differentiate $tex2html_wrap_inline73$ .

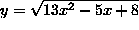SOLUTION 2 : Differentiate $tex2html_wrap_inline542$ .
( The outer layer is ``the square root'' and the inner layer is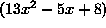 $tex2html_wrap_inline544$ . Differentiate ``the square root'' first, leaving 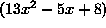$tex2html_wrap_inline544$ unchanged. Then differentiate 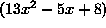$tex2html_wrap_inline544$ . ) Thus,

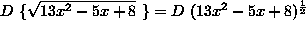
$tex2html_wrap_inline550$

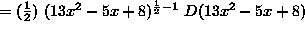
$tex2html_wrap_inline552$

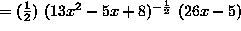
$tex2html_wrap_inline554$

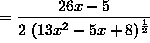
$tex2html_wrap_inline556$

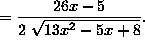
$tex2html_wrap_inline558$
Each of the following problems requires more than one application of the chain rule.

PROBLEM 12 : Differentiate $tex2html_wrap_inline93$ .

SOLUTION 12 : Differentiate $tex2html_wrap_inline750$ .
( Recall that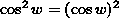 $tex2html_wrap_inline752$ , which makes ``the square'' the outer layer, NOT ``the cosine function''. In fact, this problem has three layers. The first layer is ``the square'', the second layer is ``the cosine function'', and the third layer is 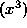$tex2html_wrap_inline754$ . Differentiate ``the square'' first, leaving ``the cosine function'' and 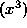$tex2html_wrap_inline754$ unchanged. Then differentiate ``the cosine function'', leaving 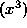$tex2html_wrap_inline754$ unchanged. Finish with the derivative of 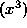$tex2html_wrap_inline754$ . ) Thus,

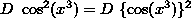
$tex2html_wrap_inline762$

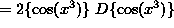
$tex2html_wrap_inline764$

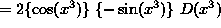
$tex2html_wrap_inline766$

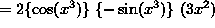
$tex2html_wrap_inline768$

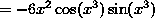
$tex2html_wrap_inline770$

PROBLEM 13 : Differentiate $tex2html_wrap_inline95$

SOLUTION 13 : Differentiate 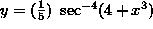$tex2html_wrap_inline772$ .

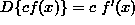( Since $tex2html_wrap_inline774$ is a MULTIPLIED CONSTANT, we will first use the rule $tex2html_wrap_inline696$ , where c is a constant. Hence, the constant $tex2html_wrap_inline774$ just ``tags along'' during the differentiation process. It is NOT necessary to use the product rule. ) Thus,

$tex2html_wrap_inline782$

( Recall that 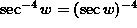$tex2html_wrap_inline784$ , which makes ``the negative four power'' the outer layer, NOT ``the secant function''. In fact, this problem has three layers. The first layer is ``the negative four power'', the second layer is ``the secant function'', and the third layer is 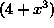$tex2html_wrap_inline786$ . Differentiate ``the negative four power'' first, leaving ``the secant function'' and 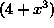$tex2html_wrap_inline786$ unchanged. Then differentiate ``the secant function'', leaving 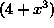$tex2html_wrap_inline786$ unchanged. 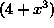Finish with the derivative of $tex2html_wrap_inline786$ . )

$tex2html_wrap_inline794$